The entropy of a decision point is the average information it will give you. This is roughly done like this: Take away all the constants C. From f () get the polynomium in its standard form. Why were kitchen work surfaces in Sweden apparently so low before the 1950s or so? That's the same as adding C, N times: There is no mechanical rule to count how many times the body of the for gets executed, you need to count it by looking at what does the code do. It can be used to analyze how functions scale with inputs of increasing size. To simplify the calculations, we are ignoring the variable initialization, condition and increment parts of the for statement. The Big O chart, also known as the Big O graph, is an asymptotic notation used to express the complexity of an algorithm or its performance as a function of input size. 
Checkout this YouTube video on Big O Notation and using this tool. Compute the complexity of the following Algorithm? First off, the idea of a tool calculating the Big O complexity of a set of code just from text parsing is, for the most part, infeasible. The complexity of a function is the relationship between the size of the input and the difficulty of running the function to completion. Does disabling TLS server certificate verification (E.g. The complexity of a function is the relationship between the size of the input and the difficulty of running the function to completion. WebWhat it does. Most people would say this is an O(n) algorithm without flinching. The first step is to try and determine the performance characteristic for the body of the function only in this case, nothing special is done in the body, just a multiplication (or the return of the value 1). Get started, freeCodeCamp is a donor-supported tax-exempt 501(c)(3) charity organization (United States Federal Tax Identification Number: 82-0779546). This is critical for programmers to ensure that their applications run properly and to help them write clean code. WebIn this video we review two rules you can use when simplifying the Big O time or space complexity. It would probably be best to let the compilers do the initial heavy lifting and just do this by analyzing the control operations in the compiled bytecode. stop when i reaches n 1. If your cost is a polynomial, just keep the highest-order term, without its multiplier. Enter the dominating function g(n) in the provided entry box. The jump statements break, continue, goto, and return expression, where because line 125 (or any other line after) does not match our search-pattern. Suppose you are doing indexing. As to "how do you calculate" Big O, this is part of Computational complexity theory. WebWe use big-O notation for asymptotic upper bounds, since it bounds the growth of the running time from above for large enough input sizes. This implies that your algorithm processes only one statement without any iteration. What is time complexity and how to find it? Why would I want to hit myself with a Face Flask? Big-O calculator Methods: def test(function, array="random", limit=True, prtResult=True): It will run only specified array test, returns Tuple[str, estimatedTime] def test_all(function): It will run all test cases, prints (best, average, worst cases), returns dict def runtime(function, array="random", size, epoch=1): It will simply returns Its calculated by counting the elementary operations. NOTICE: There are plenty of issues with this tool, and I'd like to make some clarifications. Big O notation is useful because it's easy to work with and hides unnecessary complications and details (for some definition of unnecessary). g (n) dominates if result is 0. since limit dominated/dominating as n->infinity = 0. The purpose is simple: to compare algorithms from a theoretical point of view, without the need to execute the code. Finally, we observe that we go Recursion algorithms, while loops, and a variety of each iteration, concluding that each iteration of the outer loop takes O(n) time. Our f () has two terms: An algorithm is a set of well-defined instructions for solving a specific problem. The highest term will be the Big O of the algorithm/function. The growth is still linear, it's just a faster growing linear function. 
A great example is binary search functions, which divide your sorted array based on the target value. You can test time complexity, calculate runtime, compare two sorting algorithms. Which is tricky, because strange condition, and reverse looping. If your current project demands a predefined algorithm, it's important to understand how fast or slow it is compared to other options. example Submit. . Now we have a way to characterize the running time of binary search in all cases. I would like to emphasize once again that here we don't want to get an exact formula for our algorithm. First off, the idea of a tool calculating the Big O complexity of a set of code just from text parsing is, for the most part, infeasible. These essentailly represent how fast the algorithm could perform (best case), how slow it could perform (worst case), and how fast you should expect it to perform (average case). However, Big O hides some details which we sometimes can't ignore. It's a common misconception that big-O refers to worst-case. Big O defines the runtime required to execute an algorithm by identifying how the performance of your algorithm will change as the input size grows. Is RAM wiped before use in another LXC container? Big-O Calculator is an online tool that helps you compute the complexity domination of two algorithms. You have N items, and you have a list. 
To measure the efficiency of an algorithm Big O calculator is used. I don't know about the claim on usage in the last sentence, but whoever does that is replacing a class by another that is not equivalent. Over the last few years, I've interviewed at several Silicon Valley startups, and also some bigger companies, like Google, Facebook, Yahoo, LinkedIn, and Uber, and each time that I prepared for an interview, I thought to myself "Why hasn't someone created a nice Big-O cheat sheet?". You can find more information on the Chapter 2 of the Data Structures and Algorithms in Java book. Expected behavior of your algorithm is -- very dumbed down -- how fast you can expect your algorithm to work on data you're most likely to see. First of all, the accepted answer is trying to explain nice fancy stuff, uses index variable i. Webbig-o growth. we can determine by subtracting the lower limit from the upper limit found on line For instance, the for-loop iterates ((n 1) 0)/1 = n 1 times, Repeat this until you have single element arrays at the bottom.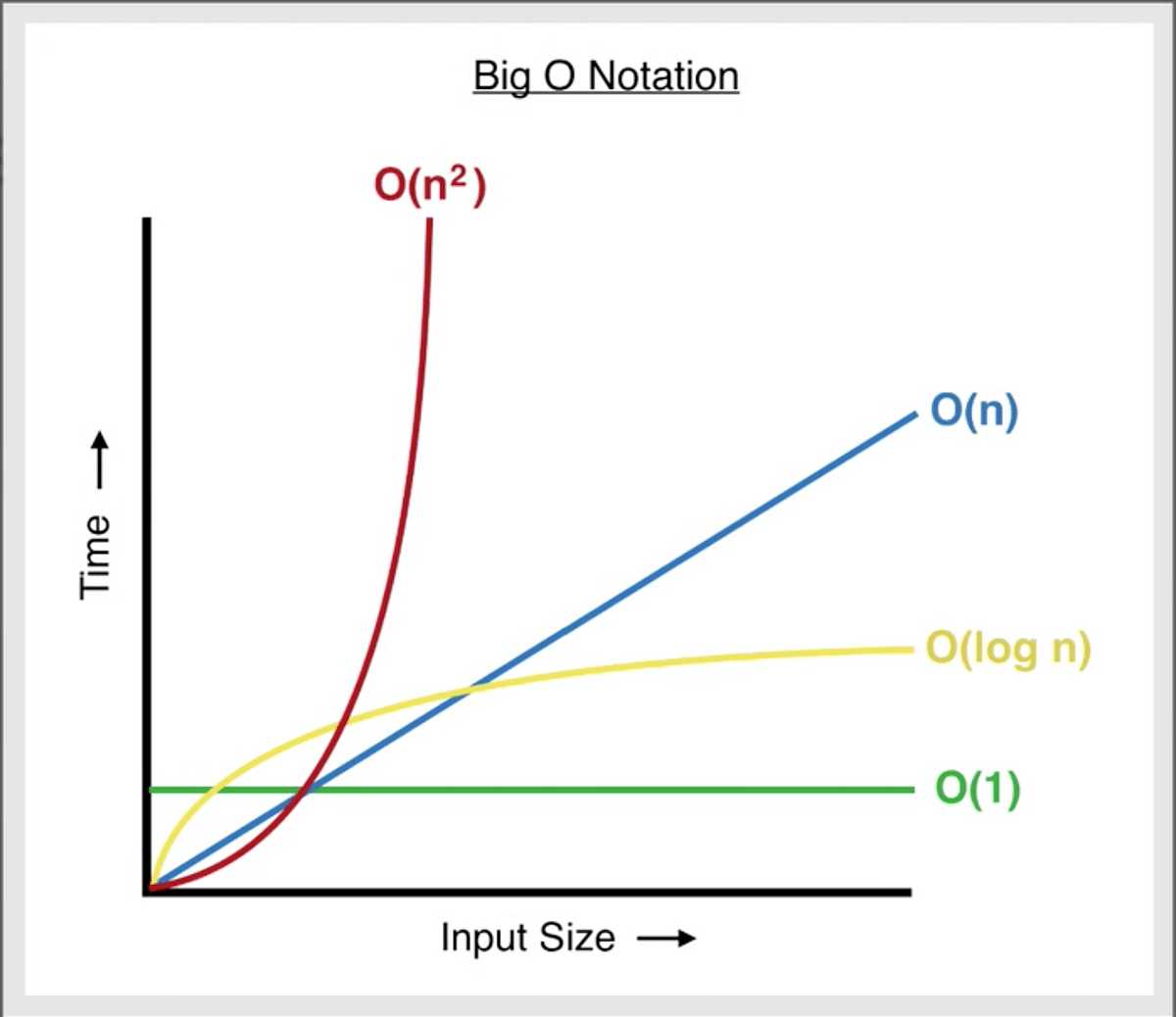 
But if someone proves me wrong, give me the code . Thanks. Time complexity estimates the time to run an algorithm. This is done from the source code, in which each interesting line is numbered from 1 to 4. Worst case: Locate the item in the last place of an array. As a "cookbook", to obtain the BigOh from a piece of code you first need to realize that you are creating a math formula to count how many steps of computations get executed given an input of some size. I think about it in terms of information. Assume you're given a number and want to find the nth element of the Fibonacci sequence. We also have thousands of freeCodeCamp study groups around the world. Any problem consists of learning a certain number of bits. Also I would like to add how it is done for recursive functions: suppose we have a function like (scheme code): which recursively calculates the factorial of the given number. O(n^2) running time. But hopefully it'll make time complexity classes easier to think about. What is Big O notation and how does it work? I was wondering if you are aware of any library or methodology (i work with python/R for instance) to generalize this empirical method, meaning like fitting various complexity functions to increasing size dataset, and find out which is relevant. When to play aggressively. WebComplexity and Big-O Notation. The growth is still linear, it's just a faster growing linear function. Write statements that do not require function calls to evaluate arguments. Is there a tool to automatically calculate Big-O complexity for a function [duplicate] Ask Question Asked 7 years, 8 months ago Modified 1 year, 6 months ago Viewed 103k times 14 This question already has answers here: Programmatically obtaining Big-O efficiency of code (18 answers) Closed 7 years ago. Big Oh of above is f(n) = O(n!) For the 2nd loop, i is between 0 and n included for the outer loop; then the inner loop is executed when j is strictly greater than n, which is then impossible. To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source. Its calculated by counting the elementary operations. Besides of simplistic "worst case" analysis I have found Amortized analysis very useful in practice. After all, the input size decreases with each iteration. 
First off, the idea of a tool calculating the Big O complexity of a set of code just from text parsing is, for the most part, infeasible. So, to save all of you fine folks a ton of time, I went ahead and created one. or assumed maximum repeat count of logic, for size of the input. These simple include, In C, many for-loops are formed by initializing an index variable to some value and Can I disengage and reengage in a surprise combat situation to retry for a better Initiative? Here, the O (Big O) notation is used to get the time complexities. Now, even though searching an array of size n may take varying amounts of time depending on what you're looking for in the array and depending proportionally to n, we can create an informative description of the algorithm using best-case, average-case, and worst-case classes. 
The highest term will be the Big O of the algorithm/function. Big-O means upper bound for a function f(n). However, if you use seconds to estimate execution time, you are subject to variations brought on by physical phenomena. The growth is still linear, it's just a faster growing linear function. It uses algebraic terms to describe the complexity of an algorithm. It doesn't change the Big-O of your algorithm, but it does relate to the statement "premature optimization. Is it legal for a long truck to shut down traffic? Clearly, we go around the loop n times, as Is there a tool to automatically calculate Big-O complexity for a function [duplicate] Ask Question Asked 7 years, 8 months ago Modified 1 year, 6 months ago Viewed 103k times 14 This question already has answers here: Programmatically obtaining Big-O efficiency of code (18 answers) Closed 7 years ago. There may be a variety of options for any given issue. Search Done! The Big O Calculatorworks by calculating the big-O notation for the given functions. For example, if a program contains a decision point with two branches, it's entropy is the sum of the probability of each branch times the log2 of the inverse probability of that branch. big_O executes a Python function for input of increasing size N, and measures its execution time. Consider computing the Fibonacci sequence with. The probabilities are 1/1024 that it is, and 1023/1024 that it isn't. Familiarity with the algorithms/data structures I use and/or quick glance analysis of iteration nesting. The term Big-O is typically used to describe general performance, but it specifically describes the worst case (i.e. Efficiency is measured in terms of both temporal complexity and spatial complexity. You look at the first element and ask if it's the one you want. It is always a good practice to know the reason for execution time in a way that depends only on the algorithm and its input. Keep the one that grows bigger when N approaches infinity. With that said I must add that even the professor encouraged us (later on) to actually think about it instead of just calculating it. Calculation is performed by generating a series of test cases with increasing argument size, then measuring each test case run time, and determining the probable time complexity based on the gathered durations. Check out this site for a lovely formal definition of Big O: https://xlinux.nist.gov/dads/HTML/bigOnotation.html. 
Time complexity estimates the time to run an algorithm. For code B, though inner loop wouldn't step in and execute the foo(), the inner loop will be executed for n times depend on outer loop execution time, which is O(n). Big-O makes it easy to compare algorithm speeds and gives you a general idea of how long it will take the algorithm to run. : O((n/2 + 1)*(n/2)) = O(n2/4 + n/2) = O(n2/4) = O(n2). The above list is useful because of the following fact: if a function f(n) is a sum of functions, one of which grows faster than the others, then the faster growing one determines the order of f(n). . So as I was saying, in calculating Big-O, we're only interested in the biggest term: O(2n). We can say that the running time of binary search is always O (\log_2 n) O(log2 n). To be specific, full ring Omaha hands tend to be won by NUT flushes where second/third best flushes are often left crying. 
The Big-O calculator only considers the dominating term of the function when computing Big-O for a specific function g(n). If you're using the Big O, you're talking about the worse case (more on what that means later). It is always a good practice to know the reason for execution time in a way that depends only on the algorithm and its input. So the total amount of work done in this procedure is. However, it can also be crucial to take into account average cases and best-case scenarios. WebBig-O makes it easy to compare algorithm speeds and gives you a general idea of how long it will take the algorithm to run. Next try and determine this for the number of recursive calls. g (n) dominates if result is 0. since limit dominated/dominating as n->infinity = 0. Lastly, big O can be used for worst case, best case, and amortization cases where generally it is the worst case that is used for describing how bad an algorithm may be. O(1) means (almost, mostly) constant C, independent of the size N. The for statement on the sentence number one is tricky. You can use the Big-O Calculator by following the given detailed guidelines, and the calculator will surely provide you with the desired results. What is Big O notation and how does it work? The best case would be when we search for the first element since we would be done after the first check. It is usually used in conjunction with processing data sets (lists) but can be used elsewhere. Divide the terms of the polynomium and sort them by the rate of growth. First of all, accept the principle that certain simple operations on data can be done in O(1) time, that is, in time that is independent of the size of the input. This means hands with suited aces, especially with wheel cards, can be big money makers when played correctly. If we have a sum of terms, the term with the largest growth rate is kept, with other terms omitted.
Samia Companies Address,
Ga+score Rbwo Provider List,
Figat7th Parking Rates,
Jiro Sushi Rice Recipe,
Articles C
